來到倒數第五天了!
也是最後一個主題遞迴Recursion

遞迴

遞迴是一種在函式內又呼叫自己的用法
通常用於解決可以分解為更簡單子問題的問題

遞迴的基本架構

基礎情況(Base Case):每一個遞迴函式都要有基本情況，是遞迴的停止條件
如果沒有基本情況的話，遞迴就會一直跑~無限循環

遞迴情況(Recursive Case)：在函式裡面又呼叫自己，每一次的呼叫都會讓問題的規模變小

接下來給大家看遞迴的簡單範例~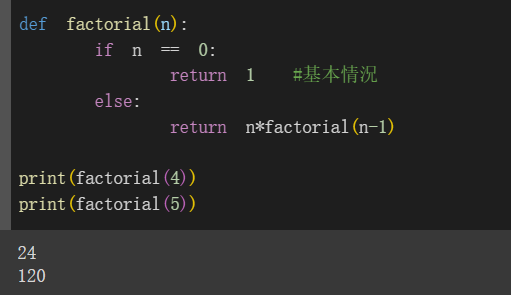

我們來看factorial這個函數
if n == 0這段就是基本情況，如果n是0，函式就回傳1，這樣遞迴就會停止
else部分的return n * factorial(n-1)，它呼叫了自己來運算(factorial(n-1))
這樣可以一直計算階乘的值，直到達到基本情況!

後面我代入4和5給大家看結果!
我用4來寫出它的過程

計算 factorial(4)

factorial(4)：不等於0，所以呼叫factorial(3)

factorial(3)：不等於0，所以呼叫factorial(2)

factorial(2)：不等於0，所以呼叫factorial(1)

factorial(1)：不等於0，所以呼叫factorial(0)

factorial(0)：等於0，所以回傳1

回傳:

factorial(1) 回傳 1 * 1 = 1

factorial(2) 回傳 2 * 1 = 2

factorial(3) 回傳 3 * 2 = 6

factorial(4) 回傳 4 * 6 = 24

以此類推!

今天遞迴介紹到這裡~
最後會用三個遞迴題目來結束這個系列!